### Establish project paths
root = '/content/drive/MyDrive/Colab_Notebooks/'
project_dir = 'experiments/'
output_dir = 'stylesheet_tests/'
project_path = root + project_dir
output_path = root + project_dir + output_dir
env_path = project_path + 'requirements.txt'1 Global settings
Visual elements and parameters I consider when establishing defaults
knitr::include_graphics("../../images/attribute_histogram_plots.png")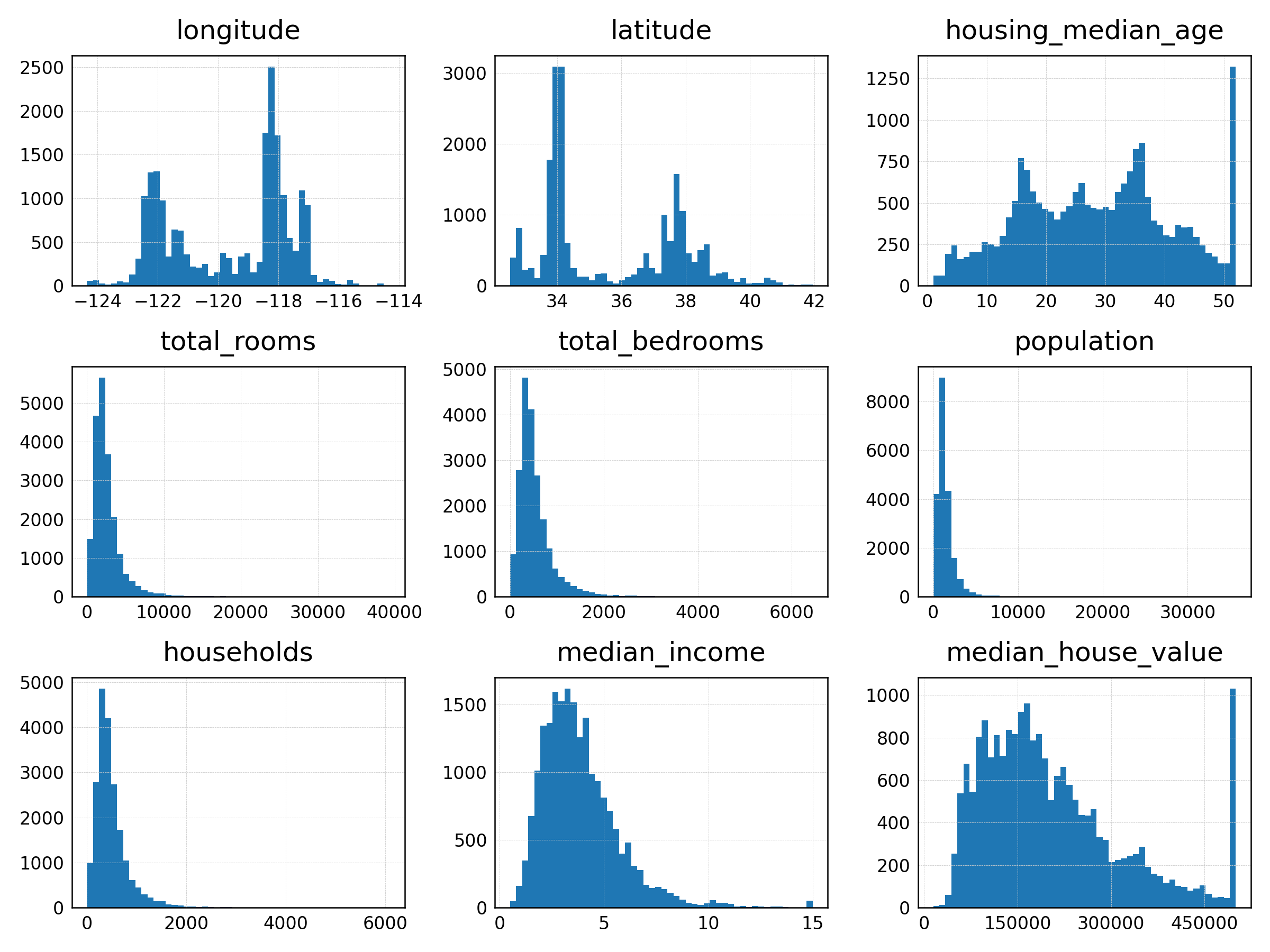
Figure 1: Pairplot of variables related to housing prices.
#> Name Age Score
#> 1 Alice 25 85
#> 2 Bob 30 92
#> 3 Charlie 22 78knitr::kable(df, caption = "Caption", digits = 2)| Name | Age | Score |
|---|---|---|
| Alice | 25 | 85 |
| Bob | 30 | 92 |
| Charlie | 22 | 78 |
Generic
text(x/y/title/tick labels/legend title/legend items): font face/sizeaxes: which to display/linewidth/minMax tick sizes/minMax tick widthsgrid: which minMax VerticalHorizontal lines to display/colour/linewidthobject: edgecolour/edgewidthcolours: discrete cycle/continuous maplegend: box/placementfigure: sizesubplots: vertical padding/horizontal paddingother: layout compactness, display quality
Additional specifications for particular objects
scatter: marker sizeline: width/continuous error colour/continuous error linewidthbar: width/between group spacing/errorbar colour/errorbar linewidth/errorbar cap widthgrouped bar: within group spacingbox: median colour/median width
Note: for each of the above, despite generic object defaults, may additionally have to specify:
- edgecolour/edgewidth
Parameters to consider manually specifying for each (sub)plot:
labels/title: on or offtick labels: rotation, which ticksaxes: limits, which ticksgrid: which linesobject: alphafigure: sizesubplots: RowColPosition arrangement, (shared) labels/titles
Typical plotting function arguments:
- data, fill variable, size variable
- plot type, error type, kernel type, regression type
- bin/sampling resolution
References - The matplotlibrc file - matplotlib.org
Note
- All lines in the matplotlibrc file start with a ‘#’, so that removing all leading ’#’s yields a valid style file
### [SCRATCH] Get fonts
from pathlib import Path
from matplotlib import font_manager as fm
from fontTools.ttLib import TTFont
# !wget 'https://github.com/google/fonts/blob/main/ofl/allison/Allison-Regular.ttf'
font_file = Path(*fm.findSystemFonts('.'))
font_file_path = Path(font_file)
# fm.fontManager.addfont(font_file_path) # [TODO] resolve this### [SCRATCH]
import os
item = 'Abel-Regular.ttf'
overwrite = 1
source_path = os.path.join('/content/', item)
output_path = os.path.join(project_path, output_dir, item)
print(f"Copying: {item} from {source_path} to {output_path}")
if os.path.isfile(source_path) or os.path.isdir(source_path):
# Check if the item already exists in the output path
if os.path.exists(output_path):
if overwrite:
# Copy the item
#!cp -rf "$source_path" "$output_path"
print(f"Successfully copied {item} ->\n{output_path}\n")
else:
print(f"Skipped: {item} already exists in {output_path}\n")
else:
# Copy the item
#!cp -rf "$source_path" "$output_path"
print(f"Successfully copied {item} to {output_path}\n")### [SCRATCH]
# !pip install pipreqs
# !pipreqs > requirements.txt --force### View path to base matplotlibrc file
import matplotlib
matplotlib.matplotlib_fname()### STYLESHEET TEMPLATE
# font.family : 'sans'### Stylesheet. Contrast with https://matplotlib.org/stable/users/explain/customizing.html#the-matplotlibrc-file
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
from matplotlib.colors import ListedColormap
## General
# Font face and sizes
mpl.rcParams['font.family'] = 'sans-serif'
# mpl.rcParams['font.sans-serif'] = "Helvetica"
mpl.rcParams['font.size'] = 8 # default font sizes
mpl.rcParams['axes.titlesize'] = 12 # large
mpl.rcParams['axes.labelsize'] = 9 # medium
mpl.rcParams['xtick.labelsize'] = 8 # medium
mpl.rcParams['ytick.labelsize'] = 8 # medium
mpl.rcParams['legend.fontsize'] = 9 # medium
mpl.rcParams['legend.title_fontsize'] = 9 # None (same as default axes)
mpl.rcParams['figure.titlesize'] = 15 # large (suptitle size)
mpl.rcParams['figure.labelsize'] = 12 # large (sup[x|y]label size)
# Spines and ticks
# mpl.rcParams['axes.spines.top'] = False
# mpl.rcParams['axes.spines.right'] = False
mpl.rcParams['axes.linewidth'] = .6
mpl.rcParams['axes.edgecolor'] = 'black'
mpl.rcParams['xtick.major.size'] = 0 # 3.5
mpl.rcParams['ytick.major.size'] = 0 # 3.5
# mpl.rcParams['xtick.major.width'] = 0.8
# mpl.rcParams['ytick.major.width'] = 0.8
# Grid
mpl.rcParams['axes.grid.which'] = 'major' # lines at {major, minor, both} ticks
mpl.rcParams['grid.linestyle'] = '--'
mpl.rcParams['grid.color'] = '#CCCCCC'
mpl.rcParams['grid.linewidth'] = 0.2
# mpl.rcParams['grid.alpha'] = 1
# Label placement
mpl.rcParams['axes.titlelocation'] = 'center' # {left, right, center}
mpl.rcParams['axes.titlepad'] = 7.5 # 6
mpl.rcParams['axes.labelpad'] = 7.5 # 4
# mpl.rcParams['xtick.major.pad'] = 3.5 # distance to major tick label in points
# mpl.rcParams['ytick.major.pad'] = 3.5
# Discrete color cycle (and continuous map)
# mpl.rcParams['axes.prop_cycle'] = mpl.cycler(color=['#1f77b4', '#ff7f0e', '#2ca02c', '#d62728'])
mpl.rcParams['axes.prop_cycle'] = mpl.cycler(color=sns.color_palette("PiYG", n_colors=6))
# Legend properties
mpl.rcParams['legend.loc'] = 'best'
mpl.rcParams['legend.frameon'] = False
mpl.rcParams['legend.loc'] = 'best'
# Legend padding
# mpl.rcParams['legend.borderpad'] = 0.4 # border whitespace
# mpl.rcParams['legend.labelspacing'] = 0.5 # vert space between legend entries
# mpl.rcParams['legend.handlelength'] = 2.0 # length of the legend lines
# mpl.rcParams['legend.handleheight'] = 0.7 # height of the legend handle
# mpl.rcParams['legend.handletextpad'] = 0.8 # space btwn legend line legend text
# mpl.rcParams['legend.borderaxespad'] = 0.5 # border btwn axes and legend edge
# mpl.rcParams['legend.columnspacing'] = 2.0 # column separation
# Space-filling object properties (e.g., polygons/circles, scatter)
mpl.rcParams['patch.edgecolor'] = 'blue' # if forced, else patch is not filled
mpl.rcParams['patch.force_edgecolor'] = 1
mpl.rcParams['patch.linewidth'] = 0 # edgewidth (.5)
## Specific objects
# Scatter properties
# mpl.rcParams['scatter.edgecolors'] = 'black'
# Line properties
mpl.rcParams['lines.markersize'] = 5
mpl.rcParams['lines.linewidth'] = 2
# Bar properties
# mpl.rcParams['bar.width'] = 0.8
# Error properties
mpl.rcParams['errorbar.capsize'] = 1
# mpl.rcParams['errorbar.color'] = 'black'
# mpl.rcParams['errorbar.linewidth'] = 1.5
# Box properties
# box
mpl.rcParams['boxplot.boxprops.linewidth'] = 0 # box outline (0.5)
# mpl.rcParams['boxplot.boxprops.color'] = 'none' # 'black' (?)
# box line to cap
mpl.rcParams['boxplot.whiskerprops.linewidth'] = .65
mpl.rcParams['boxplot.whiskerprops.linestyle'] = '--'
# mpl.rcParams['boxplot.whiskerprops.color'] = 'black' # (?)
# box cap line
mpl.rcParams['boxplot.capprops.linewidth'] = .75
# mpl.rcParams['boxplot.capprops.color'] = 'black' # (?)
# box median line
mpl.rcParams['boxplot.medianprops.linewidth'] = 1
mpl.rcParams['boxplot.medianprops.linestyle'] = '-'
# mpl.rcParams['boxplot.medianprops.color'] = 'black' # (?)
mpl.rcParams['boxplot.meanprops.linewidth'] = 1
mpl.rcParams['boxplot.meanprops.linestyle'] = '-'
# mpl.rcParams['boxplot.meanprops.color'] = 'black' # (?)
# box scatter
mpl.rcParams['boxplot.flierprops.markerfacecolor'] = 'none'
mpl.rcParams['boxplot.flierprops.markeredgewidth'] = .65
mpl.rcParams['boxplot.flierprops.marker'] = 'o'
# mpl.rcParams['boxplot.flierprops.markersize'] = 6 # (?)
# mpl.rcParams['boxplot.flierprops.linewidth'] = 0 # (?)
# mpl.rcParams['boxplot.flierprops.markeredgecolor'] = 'black' # (?)
# mpl.rcParams['boxplot.flierprops.color'] = 'black' # (?)
## Figure padding
# Figure layout
mpl.rcParams['figure.autolayout'] = True # auto- make plot elements fit on fig
mpl.rcParams['figure.constrained_layout.use'] = True # apply tight layout
# Subplot padding (all dims are a fraction of the fig width and height).
# Not compatible with constrained_layout.
# mpl.rcParams['figure.subplot.left'] = .125 # left side of subplots of fig
# mpl.rcParams['figure.subplot.right'] = 0.9 # right side of subplots of fig
# mpl.rcParams['figure.subplot.bottom'] = 0.11 # bottom of subplots of fig
# mpl.rcParams['figure.subplot.top'] = 0.88 # top of subplots of figure
# mpl.rcParams['figure.subplot.wspace'] = 0.2 # w reserved space btwn subplots
# mpl.rcParams['figure.subplot.hspace'] = 0.2 # h reserved space btwn subplots
# Constrained layout padding. Not compatible with autolayout.
# mpl.rcParams['figure.constrained_layout.h_pad'] = 0.04167
# mpl.rcParams['figure.constrained_layout.w_pad'] = 0.04167
# Constrained layout spacing between subplots, relative to the subplot sizes.
# Much smaller than for tight_layout (figure.subplot.hspace, figure.subplot.wspace)
# as constrained_layout already takes surrounding text (titles, labels, # ticklabels)
# into account. Not compatible with autolayout.
# mpl.rcParams['figure.constrained_layout.hspace'] = 0.02
# mpl.rcParams['figure.constrained_layout.wspace'] = 0.02
## Other
# Figure size and quality
mpl.rcParams['figure.dpi'] = 100 # [NOTE] alters figure size
mpl.rcParams['figure.figsize'] = (5, 5) # (6, 4), (6.4, 4.8)
# Figure saving settings
mpl.rcParams['savefig.transparent'] = True
mpl.rcParams['savefig.format'] = 'png'
mpl.rcParams['savefig.dpi'] = 330
#%config InlineBackend.figure_format = 'svg' # set inline figure format/quality2 Colours
[TODO]
Colour palette generator utilities
[TODO] [def] Continuous generators:
(1 H nodes) Monchromatic (linear L)
- args: 1 H node, optional n L steps from it
- example: blues
- utility: topological
- use cases: surface/distribution/contour plot
(~2-6 H nodes) Sequential (constant L):
- args: 2-6 H nodes, optional n(k - 1) transition steps between them
- example: viridis/plasma
- utility: topological
- use cases: surface/distribution/contour plot
(2 H nodes) Diverging (triangular L):
- args: 2 H nodes, optional n*2 ascending/descending L steps between them
- example: PiYG/RdBu
- utility: 1D bipolar scale/2D binary probability surface
- use cases: heatmap, classifier decision surface
(~3-6 H nodes) Sequential diverging (~triangular L)
- args: k H nodes, optional n(k - 1)*2 ascending/descending L steps between them
- example: ~gnuplot2/gist_ncar/gist_rainbow/jet
- utility: 1D multipolar scale
- use cases: heatmap with 1+ intermediate nodes
/ (~6 H nodes) Spectral (~constant L, cyclic /H)
- example: hsv
- utility: multiclass probability surface (using class probability-weighted H nodes)
- ues cases: multiclass classifier decision surface
[TODO] [def] Discrete generators:
(k H nodes) Discrete (~constant L)
- args: k H nodes
- example: tab10/Dark2
- utility: discrete objects with no within-group levels OR groups of objects with within-group levels but no order
- use cases: k objects (lines/hists/bars/boxplots) for k categories OR m objects (within groups) for m levels
(k H nodes) Discrete monochromatic (~constant L between * linear L within)
- args: k H nodes, optional n*k L steps from each node
- example: tab20/paired > tab20c/tab20b
- utility: discrete groups of objects with a within-group order and aim to highlight between-group differences
- use cases: (group * time period) * value grouped objects (lines/hists/bars/boxplots)
Colour generator utillity
Given (a) any H value and k-iary scheme / (b) H/set of H values and integer k: - (a) [def] return complimentary/triad/square/k-iary H nodes - (b) [def] return k quantized H nodes
[TODO] For all of the above: - args: accept k colours and optional n steps - convert inputs to H values [0-359] - (maximize S/L of input args) - if multiple H nodes passed, quantize so each evenly spaced on colorwheel - return: k H nodes (+ either colourmap or discrete colourset) - plot: H nodes on colourwheel (+ colourbar)
[TODO] Other: - demo how to convert any map hsl values
[REF] Tools - Adobe Colorwheel
Matplotlib - Choosing Colormaps - Creating Colormaps
Other libraries - seaborn - CMasher - Colormaps - Palettable
Theory - Standard color space: HSL and HSV - Wikipedia - Perceptually uniform color space: HCL - hclwizard - Human-friendly HSL! : HSLuv - HSLuv.org
Other - Reference of good perceptual palettes: HCL-Based Color Palettes - colorspace
#!pip install cmasher### Continuous maps
# (1) Monochromatic (1 H, linear L)
#import cmasher as cmr
#cmr.get_sub_cmap('Blues_r', 0, 1, N=20)#cmr.get_sub_cmap('Greens_r', 0, 1, N=20)# (2) Sequential (multiple H, constant L)
#cmr.get_sub_cmap('plasma', 0, 1, N=20)#cmr.get_sub_cmap('cmr.chroma', 0.2, .8, N=20)### Constructing monochromatic (rot=.1)/sequential/cyclic (rot=1) maps w/ linear L
# starting H [0, 3] (ROYGBIV = 3/7*h), rotations around hue wheel (int)
# dark/light (intensity of darkest/lightest color in palette) [0, 1] or gamma
ListedColormap(sns.cubehelix_palette(start=(3/7)*1, rot=.1, reverse=True, gamma=.7,
# dark=.25, light=.85,
n_colors=20, as_cmap=False))# (3) Diverging (~2 H, triangular L)
#cmr.get_sub_cmap('PiYG', 0, 1, N=20)#cmr.get_sub_cmap('Spectral', 0, 1, N=20)# (4) Sequentially diverging (3-6 H, ~triangular L)
#cmr.get_sub_cmap('gnuplot', 0, 1, N=20)### Constructing diverging/sequentially diverging map
# starting/ending H [0, 359], S [0, 100], L [0, 100]
n_colors = 50
palette_1 = sns.diverging_palette(h_neg=100, h_pos=200, s=100, l=50, n=n_colors, as_cmap=False)
palette_1 = ListedColormap(palette_1)
palette_1palette_2 = sns.diverging_palette(h_neg=200, h_pos=300, s=100, l=50, n=n_colors, as_cmap=False)
palette_2 = ListedColormap(palette_2)
palette_2# Combine
import numpy as np
palette_combined = np.vstack((
palette_1(np.linspace(0, 1, n_colors)),
palette_2(np.linspace(1/n_colors, 1, n_colors - 1))))
ListedColormap(palette_combined, name='GrBlPu')# (5) Spectral (cyclic H, ~constant L)
ListedColormap(sns.color_palette("husl", n_colors=10, as_cmap=False))#cmr.get_sub_cmap('hsv', 0, 1, N=20)### Discrete maps
#cmr.get_sub_cmap('tab20b', 0, 1, N=20)
# plt.cm.tab20b### Constructing discrete monochromatic map (hue-grouped truncated discrete map)
n_groups = 3
n_bars = 3
colors = plt.cm.tab20b((
[0,1,2,
4,5,6,
16,17,18])).reshape(n_groups, n_bars, 4)
ListedColormap(colors.reshape(n_groups * n_bars, 4))
# ListedColormap(colors[0, :])### Obtain hex/rgb string codes for specified colourmap
# return_fmt {hex, float=rgb}
#cmr.take_cmap_colors('cmr.chroma', cmap_range=(0, 1), N=20, return_fmt='float')###
# [TODO] legend has 1st colour of each group; xaxis has rotated labels of 3*3
import matplotlib.pyplot as plt
import numpy as np
species = ("Adelie", "Chinstrap", "Gentoo")
data = {
'Bill Depth': (18.35, 18.43, 14.98),
'Bill Length': (38.79, 48.83, 47.50),
'Flipper Length': (189.95, 195.82, 217.19),
}
x = np.arange(len(species)) # the label locations
width = 0.2 # the width of the bars
multiplier = 0
fig, ax = plt.subplots(layout='constrained')
for group, (attribute, measurement) in enumerate(data.items()):
offset = width * multiplier
rects = ax.bar(x + offset, measurement, width, alpha=.85,
label=attribute.lower().capitalize(),
color=colors[:, group])
ax.bar_label(rects, padding=3)
multiplier += 1
ax.grid(axis='y'); ax.legend(ncols=3)
ax.set_ylim(0, 250)
ax.set_xticks(x + width, species)
ax.set_ylabel('Length (mm)')
ax.set_title('Whitepaper plot')
plt.show()3 Tools for data representation & manipulation
### [def] Utilities for visualizing df and LA operations
# [REF] Vanderplas; [MB] adapted to handle numpy arrays
import numpy as np
import numpy.linalg as la
import pandas as pd
class display(object):
"""Display HTML representation of multiple objects"""
template = """<div style="float: left; padding: 10px;">
<p style='font-family:"Courier New", Courier, monospace'>{0}{1}
"""
def __init__(self, *args):
self.args = args
def __repr__(self):
return '\n\n'.join(
'\n' + '\033[1m' + a + '\033[0m'
+ '\n' + ' ' + repr(np.shape(eval(a))) + ' '
+ '\n' + repr(np.round(eval(a), 2))
for a in self.args
)
def make_df(cols, ind):
"""Quickly make a DataFrame"""
data = {c: [str(c) + str(i) for i in ind]
for c in cols}
return pd.DataFrame(data, ind)### Examples: Visualizing df operations
df1 = make_df('AB', [1, 2])
df2 = make_df('AB', [3, 4])
display('df1', 'df2', 'pd.concat([df1, df2])')### Examples: Visualizing matrix operations
# Matrix algebra & operations
X = np.array([[1, 2, 3], [4, 5, 6]])
Y = np.array([[1, 2, 3], [4, 5, 6]])
display('X', 'Y.T', 'X @ Y.T', 'la.inv(X @ Y.T)', 'la.det(X @ Y.T)')# Outer products
x = np.array([1, 2])
y = x + 1
display('x', 'y', 'np.outer(x, y)')# Eigendecomposition
X_square = np.vstack((X, np.array([7, 8, 9])))
eig, Evec = la.eig(X_square)
Eig = np.diag(eig)
display('X_square', 'Eig', 'Evec')# Matrix decomposition
U, d, V_T = la.svd(X_square)
D = np.diag(d)
display('X_square', 'U', 'D', 'V_T')# Forming tensors: From vectors
x_vec = x[:, np.newaxis]
x_ten = x_vec[:, :, np.newaxis]
display('x', 'x_vec', 'x_ten')# Forming tensors: From matrices
X_3D1 = X[:, :, np.newaxis]
X_3D2 = X[:, np.newaxis, :]
X_3D3 = X[np.newaxis, :, :]
display('X', 'X_3D1', 'X_3D2', 'X_3D3')# Tensor broadcasting: From vectors
c = np.array([0, 1, 2])
display('x_vec', 'x_ten', 'c', 'x_ten - c')# Tensor broadcasting: From matrices
display('X', 'X_3D1', 'c', 'X_3D1 - c')# Reshaping & aggregating: From vectors
display('x_vec', 'c', 'x_ten - c',
'(x_ten - c) ** 2',
'np.sum((x_ten - c) ** 2, axis=1)')# Reshaping & aggregating: From tensors
# [TODO] add tensor dot product for summation over arbitrary dims
display('X', 'c', 'X_3D1 - c',
'(X_3D1 - c) ** 2',
'((X_3D1 - c) ** 2).reshape(len(X), 1, -1)',
'np.sum(((X_3D1 - c) ** 2).reshape(len(X), 1, -1), axis=1)') # EATS empty 1st dim4 Tools for matrix visualization
### [def] Tools for visualizing LA operations
import numpy as np
import numpy.linalg as la
import matplotlib.pyplot as plt
from matplotlib.patches import Polygon
# [NOTE] attempted to resolve pyplot matrix rendering issues
# !pip install array_to_latex
# import array_to_latex as a2l
# mpl.rcParams['text.usetex'] = True
# mpl.rcParams['text.latex.preamble'] = r'\usepackage{{amsmath}}'
# plt.rcParams["text.latex.preamble"].join([
# r"\usepackage{dashbox}",
# r"\setmainfont{xcolor}"])
# plt.rcParams.update({"text.usetex": True})
# # [REF] https://inakleinbottle.com/posts/formatting-matrices-with-python/
def format_matrix(matrix, environment="pmatrix", formatter=str):
"""Format a matrix using LaTeX syntax"""
if not isinstance(matrix, np.ndarray):
try:
matrix = np.array(matrix)
except Exception:
raise TypeError("Could not convert to Numpy array")
if len(shape := matrix.shape) == 1:
matrix = matrix.reshape(1, shape[0])
elif len(shape) > 2:
raise ValueError("Array must be 2 dimensional")
body_lines = [" & ".join(map(formatter, row)) for row in matrix]
body = "\\\\\n".join(body_lines)
return f"""\\begin{{{environment}}}
{body}
\\end{{{environment}}}"""
# [REF] Geron
def plot_vector2d(vector2d, origin=[0, 0], **options):
return plt.arrow(origin[0], origin[1], vector2d[0], vector2d[1],
linewidth=1, head_width=0.1,
head_length=0.15, length_includes_head=True,
**options)
def plot_transformation(P_before, P_after, text_before, text_after,
axis=[0, 5, 0, 4], arrows=False, display_mapping=None):
if arrows:
for vector_before, vector_after in zip(P_before.T, P_after.T):
plot_vector2d(vector_before, color="blue", linestyle="--")
# plot_vector2d(vector_before, color="blue", linestyle="-")
plot_vector2d(vector_after, color="red", linestyle="-")
if display_mapping is not None:
# M_before = r'$\begin{bmatrix} ' + '\\'.join([' & '.join(map(str, row)) for row in P_before]) + '\end{bmatrix}$'
plt.text(axis[1]*.7, axis[3]*.7,
f"{format_matrix(P, environment='bmatrix')}",
bbox=dict(facecolor='white', edgecolor='white', boxstyle='round,pad=0.3'),
fontsize=9, color="black")
plt.gca().add_artist(Polygon(P_before.T, alpha=0.2))
plt.gca().add_artist(Polygon(P_after.T, alpha=0.3, color="r"))
plt.plot(P_before[0], P_before[1], "b--", alpha=0.5)
plt.plot(P_after[0], P_after[1], "r--", alpha=0.5)
plt.text(P_before[0].mean(), P_before[1].mean(), text_before,
fontsize=12, color="blue")
# plt.text(P_before[0].max()*.9, P_before[1].max()*.9, text_before,
# fontsize=12, color="blue")
plt.text(P_after[0].mean(), P_after[1].mean(), text_after,
fontsize=12, color="red")
plt.axis(axis)
plt.gca().set_aspect("equal")
plt.grid()### Examples: Vectors
u = np.array([2, 5])
v = np.array([3, 1])
plt.subplots(figsize=(4,4))
plot_vector2d(u, color="r")
plot_vector2d(v, color="b")
plot_vector2d(v, origin=u, color="b")
plot_vector2d(u, origin=v, color="r")
plot_vector2d(u+v, color="g")
plt.axis([0, 6.5, 0, 6.5])
plt.gca().set_aspect("equal")
plt.text(0.7, 3, "u", color="r", fontsize=12)
plt.text(4, 3, "u", color="r", fontsize=12)
plt.text(1.8, 0.2, "v", color="b", fontsize=12)
plt.text(3.1, 5.6, "v", color="b", fontsize=12)
plt.text(2.4, 2.5, "u+v", color="g", fontsize=12)
plt.grid()
plt.show()### Examples: Matrices
# [def] Helper to get min & max coordinates of start & end matrices
def mat_minmax_coords(*matrices, square=False):
stacked_matrix = np.hstack(matrices)
xy_min = np.min(stacked_matrix, axis=1) * 1.1
xy_max = np.max(stacked_matrix, axis=1) * 1.1
axis = [xy_min[0], xy_max[0], xy_min[1], xy_max[1]]
if square:
axis_lengths = [xy_max[0] - xy_min[0], xy_max[1] - xy_min[1]]
scale_factor = max(axis_lengths)/axis_lengths
axis = axis * np.repeat(scale_factor, 2)
return axis
# Starting matrix
# P = np.array([[3.0, 4.0, 1.0, 4.6], [0.2, 3.5, 2.0, 0.5]]) # non-convex shape
# P = np.array([[0.0, 4.0, 6.0, 2.0], [0.0, 0.0, 5.0, 5.0]]) # neater shape
P = np.array([[0, 0, 1, 1], [0, 1, 1, 0]]) # square
P = P / 2
fig, axs = plt.subplots(2,2, figsize=(8,8))
# Scale
P_rescaled = .6 * P
plt.sca(axs[0,0]) # [0, 3.5, 0, 3.5]
plot_transformation(P, P_rescaled, "$P$", "$0.6 P$",
axis=mat_minmax_coords(P, P_rescaled, square=0),
arrows=False)
# Rotate
angle30 = 30 * np.pi / 180 # angle in radians
angle120 = 120 * np.pi / 180 # angle in radians
V = np.array([
[np.cos(angle30), np.sin(angle30)],
[np.cos(angle120), np.sin(angle120)]])
P_rotated = V @ P
plt.sca(axs[0,1]) # [-1.5, 4, -1.5, 4]
plot_transformation(P, P_rotated, "$P$", "$V_{rotate} P$",
axis=mat_minmax_coords(P, P_rotated, square=0),
display_mapping=V)
# Shear
F_shear = np.array([[1, 1.5], [0, 1]])
P_sheared = F_shear @ P
plt.sca(axs[1,0]) # [0, 7, 0, 7]
plot_transformation(P, P_sheared, "$P$", "$F_{shear} P$",
axis=mat_minmax_coords(P, P_sheared, square=0))
# Horizontal reflection
F_reflect = np.array([[1, 0], [0, -1]])
P_reflected = F_reflect @ P
plt.sca(axs[1,1]) # [-3, 4, -3, 4]
plot_transformation(P, P_reflected, "$P$", "$F_{reflect} P$",
axis=mat_minmax_coords(P, P_reflected, square=0))
plt.show()### Example: SVD
# M = np.array([[1, 1.5], [0, 1]]) # F_shear
M = (np.array([[1, 1.5], [0, 1]]))*-1
Square = np.array([
[0, 0, 1, 1],
[0, 1, 1, 0]])
U, d, V_T = la.svd(M) # 𝜎/Σ_diag, Σ
D = np.diag(d)
assert np.any(np.round(U @ D @ V_T, 1) == np.round(M, 1))# SVD
fig, axs = plt.subplots(1, 3, figsize=(9,6))
axis = mat_minmax_coords(
Square, V_T @ Square, D @ V_T @ Square, U @ D @ V_T @ Square, square=True)
plt.sca(axs[0]) # no need to explicitly plot with axs handle for custom plotter
plot_transformation(Square, V_T @ Square, "$Square$", r"$V^T \cdot Square$",
axis=axis)
plt.title('$(V^T) \cdot Square$')
plt.sca(axs[1])
plot_transformation(V_T @ Square, D @ V_T @ Square,
r"$V^T \cdot Square$", r"$\Sigma \cdot V^T \cdot Square$",
axis=axis)
plt.title('$(\Sigma \cdot V^T) \cdot Square$')
plt.sca(axs[2])
plot_transformation(D @ V_T @ Square, U @ D @ V_T @ Square,
r"$\Sigma \cdot V^T \cdot Square$",
r"$U \cdot \Sigma \cdot V^T \cdot Square$",
axis=axis)
plt.title('$(U \cdot \Sigma \cdot V^T) \cdot Square$')
# plt.suptitle('SVD')
# plt.tight_layout()
plt.show()5 Preliminary tests
### [def] Generate B/W image
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd
np.random.seed(19680801) # seed random number generator
def generate_stripe_image(size, stripe_nr, vertical = True):
"""Generate random (black) square image w/ `stripe_nr` (white) stripes"""
img = np.zeros((size, size, 1), dtype = "uint8") # init size^2 img of 0's
for i in range(0, stripe_nr):
x, y = np.random.randint(0, size, 2) # gen 2 rand int btwn 0 & size
l = np.int(np.random.randint(y, size, 1)) # rand int btwn y & size
if (vertical): # set to True by default
img[y:l, x, 0] = 255 # add vertical line from y:l in rand col x
else:
img[x, y:l, 0] = 255 # horizontal line in row x
return img### [fig] Example: Plot image
# plot example image for reference
img = generate_stripe_image(50, 10, vertical = True)
plt.imshow(img[:, :, 0], cmap = 'gray')### Generate training and validation sets
n_img = 1000
# n_stripes = 10
# img_size = 50
# initialize empty arrays to store training/validation sets
X_train = X_val = np.empty([n_img, 50, 50, 1])
vert = True # initially generate vertical images
n_vert = .5*n_img
## generate images
for i in range(np.shape(X_train)[0]):
# start generating horizontal images half-way through loop
if i == n_vert - 1:
vert = False
X_train[i, :, :, :] = generate_stripe_image(50, 10, vert)
X_val[i, :, :, :] = generate_stripe_image(50, 10, vert)
## (standard) normalize training and validation sets (based on training data)
X_mean = np.mean(X_train, axis = 0)
X_std = np.std(X_train, axis = 0) + 1e-7 # to deal w/ potential sd's of 0
X_train = (X_train - X_mean) / X_std
X_val = (X_val - X_mean) / X_std### Store true class labels (0 = vert. stripes; 1 = horiz.)
Y_train = np.zeros(500)
Y_train = Y_val = np.append(Y_train, np.ones(500))# Basicsfig, ax = plt.subplots()
ax.plot([1, 2, 3], [4, 5, 6], label='Example line 1')
ax.plot([1, 1.5, 2], [4, 5, 6], label='Example line 2')
ax.scatter([1, 2, 3], [4, 5, 6])
ax.scatter([1, 1.5, 2], [4, 5, 6])
ax.grid(); ax.legend()
ax.set_xlim(.75,3.25); #ax.set_ylim(0,3)
ax.set_xticks([1,1.5,2,2.5,3]); #ax.set_yticks([1,2,3])
ax.set_xlabel('$x$'); ax.set_ylabel('$y$')
ax.set_title('Lines & scatter')
plt.show()# [TODO] compute bar heights from randomly generated averages & add error bar
# fig, ax = plt.subplots(figsize=(6/1.2,4*1.2))
fig, ax = plt.subplots(layout='constrained')
ax.bar([1, 2, 3], [4, 5, 6], label='Example bar 1', width=.3, alpha=.85)
ax.bar([1.5, 2.5], [4, 6], label='Example bar 2', width=.3, alpha=.85)
ax.grid(which='major', axis='y'); ax.legend()
ax.set_xticks([1,2,3])
ax.set_xlabel('$x$'); ax.set_ylabel('$y$')
ax.set_title('Bars')
# plt.tight_layout()
plt.show()### Pivot table for numeric column aggregated wrt 2 cats (group/level)
# [TODO] move to data exploration, above grouping/joins
import seaborn as sns
import pandas as pd
# Load the tips dataset
tips = sns.load_dataset("tips")
# Specify the categorical variables for levels and groups
level_variable = "sex"
group_variable = "day"
# Create a pivot table to structure the data
pivot_table = tips.pivot_table(values="total_bill", index=level_variable, columns=group_variable, aggfunc="mean")
pivot_table### Pivot table for num column w/ non-aggregated values wrt 2 cats (group/level)
# For quickly plotting group comparisons
# [TODO] move to data exploration, above grouping/joins
import seaborn as sns
import pandas as pd
# Load the tips dataset
tips = sns.load_dataset("tips")
# Specify the categorical variables for levels and groups
level_variable = "sex"
group_variable = "day"
# Group by the specified variables and collect total_bill values as arrays
grouped_data = tips.groupby([level_variable, group_variable])["total_bill"].apply(list).unstack()
# Display the resulting DataFrame
grouped_data### Stat + CI for num column w/ non-aggregated values wrt 2 cats (group/level)
# For quickly obtaining stats and err for group comparisons
# [TODO] move to data exploration, above grouping/joins
import numpy as np
import pandas as pd
from scipy import stats
# Assume grouped_data is a DataFrame with multi-index (group, level) and values as arrays
# Replace 'total_bill' with the actual column name containing arrays
grouped_data = tips.groupby(['sex', 'day'])['total_bill'].apply(np.array)
# Function to calculate mean and confidence interval
def calculate_mean_ci(data):
# Convert non-numeric values to NaN and drop them
numeric_data = pd.Series(data).apply(pd.to_numeric, errors='coerce').dropna()
if len(numeric_data) > 0:
mean = np.mean(numeric_data)
ci = stats.t.interval(0.95, len(numeric_data) - 1, loc=np.mean(numeric_data), scale=stats.sem(numeric_data))
return mean, ci
else:
return np.nan, (np.nan, np.nan)
# Apply the function to each group
result_list = []
for (group, level), data in grouped_data.items():
mean, ci = calculate_mean_ci(data)
result_list.append({
'Group': group,
'Level': level,
'Mean': mean,
'Confidence Interval': ci
})
# Display the list of means and confidence intervals
for result in result_list:
print(result)# [TODO] add option to plot sigbars for within group comparisons instead of btwn
# [TODO] add option to plot sigbars for betwn group comps of particular level
# [TODO] check accuracy of stats
# [TODO] clean up
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
from itertools import combinations
# Specify the number of groups and bars per group
N_GROUPS = 4
N_LEVELS = 3
# Generate or use actual data for averages and confidence intervals
data = np.random.normal(loc=5, scale=1.0, size=(N_GROUPS, N_LEVELS, 10)) # Adjusted the number of samples
# Modify a couple of bar values to demonstrate significant differences
data[0, 0, :] += 2.5 # Increase the first bar in the first group
data[2, 2, :] -= 2.5 # Decrease the third bar in the third group
# Calculate averages and confidence intervals
averages = np.mean(data, axis=2)
conf_intervals = np.zeros_like(averages, dtype=float)
for group_idx in range(N_GROUPS):
for level_idx in range(N_LEVELS):
interval = stats.t.interval(0.95, len(data[group_idx, level_idx]) - 1,
loc=np.mean(data[group_idx, level_idx]),
scale=stats.sem(data[group_idx, level_idx]))
conf_intervals[group_idx, level_idx] = np.abs(interval[1] - averages[group_idx, level_idx]) # Use upper bound
# Plot grouped bars with confidence intervals
width = 0.2
colors = plt.cm.viridis(np.linspace(0, 1, N_LEVELS))
line_thickness = 0.7 # Adjust the line thickness
stagger_amount = 0.8 # Increased the stagger amount
fig, ax = plt.subplots()
for level_idx in range(N_LEVELS):
bars = ax.bar(np.arange(N_GROUPS) + level_idx * width - (width * (N_LEVELS - 1) / 2),
averages[:, level_idx],
yerr=conf_intervals[:, level_idx],
width=width,
alpha=0.85,
capsize=3,
color=colors[level_idx],
label=f'Level {level_idx + 1}',
error_kw={'elinewidth': line_thickness}) # Set the line thickness for error bars
# Set labels and title
ax.set_xlabel('Groups')
ax.set_ylabel('Values')
ax.set_title('Grouped Bars with Confidence Intervals')
# Set x-axis ticks and labels
group_labels = [f'Group {i}' for i in range(1, N_GROUPS + 1)]
ax.set_xticks(np.arange(N_GROUPS))
ax.set_xticklabels(group_labels)
# Add legend
ax.legend(title='Levels', bbox_to_anchor=(1.05, 1), loc='upper left')
# Add staggered significance bars and asterisks for select between-group comparisons
significance_level = 0.05
stagger_index = 0
for comb in combinations(range(N_GROUPS), 2):x
group1_center = ax.get_xticks()[comb[0]]
group2_center = ax.get_xticks()[comb[1]]
t_stat, p_value = stats.ttest_ind(data[comb[0], :, :].flatten(), data[comb[1], :, :].flatten())
if p_value < significance_level:
tallest_bar_height = np.max(averages) + np.max(conf_intervals) + 0.5
significance_height = tallest_bar_height + np.max(conf_intervals) * 0.07 + stagger_index * stagger_amount # Adjust the stagger amount
# Plot staggered horizontal lines aligned with the midpoints of the compared groups
ax.plot([group1_center, group2_center],
[significance_height] * 2, color='black', lw=line_thickness)
# Plot asterisks aligned with the center of the significance bars
asterisks = '*' * sum([p_value < alpha for alpha in [0.01, 0.001, 0.0001]])
ax.text((group1_center + group2_center) / 2, significance_height,
asterisks, ha='center', va='bottom', fontsize=10)
stagger_index += 1 # Increment the index for staggered bars
# Print significant comparisons, t-test results, and sample sizes
sample_size1 = len(data[comb[0], :, :].flatten())
sample_size2 = len(data[comb[1], :, :].flatten())
print(f'Significant comparison between {group_labels[comb[0]]} and {group_labels[comb[1]]}: '
f'p-value = {p_value}, \nt-statistic = {t_stat}, '
f'Sample Size: {group_labels[comb[0]]} = {sample_size1}, {group_labels[comb[1]]} = {sample_size2}\n')
# Show the plot
ax.grid(axis='y')
plt.tight_layout()
plt.show()import seaborn as sns
from pandas.plotting import scatter_matrix
from matplotlib.ticker import FormatStrFormatter
data = sns.load_dataset("iris")
data_ = data.rename(columns=lambda name: name.replace('_', ' ').capitalize())
fig, axs = plt.subplots()
axs = scatter_matrix(data_, ax=axs, diagonal='hist', alpha=.75,
hist_kwds=dict(alpha=.75),
)
# Iterate through the axes to set the y-axis formatter
for ax in axs.flatten():
# ax.yaxis.set_major_formatter(FormatStrFormatter('%05.2f'))
ax.yaxis.set_major_formatter(FormatStrFormatter('%.2f'))
ax.xaxis.set_major_formatter(FormatStrFormatter('%.1f'))
ax.tick_params(axis='both', labelsize=7)
ax.xaxis.label.set_size(8)
ax.yaxis.label.set_size(8)
# ax.grid()
fig.suptitle("Scatter matrix")
plt.show()# [TODO] Add example where axes flipped so text horizontal with bars
import matplotlib.pyplot as plt
import numpy as np
species = ("Adelie", "Chinstrap", "Gentoo")
penguin_means = {
'Bill Depth': (18.35, 18.43, 14.98),
'Bill Length': (38.79, 48.83, 47.50),
'Flipper Length': (189.95, 195.82, 217.19),
}
x = np.arange(len(species)) # the label locations
width = 0.2 # the width of the bars
spacing = 0.009 # the space between bars within groups
multiplier = 0
with sns.color_palette('viridis', n_colors=3, as_cmap=False):
# color=ListedColormap(plt.cm.tab20b((np.arange(0,9))))
fig, ax = plt.subplots(layout='constrained')
for attribute, measurement in penguin_means.items():
offset = (width + spacing) * multiplier
rects = ax.bar(x + offset, measurement, width, alpha=.85,
label=attribute.lower().capitalize())
ax.bar_label(rects, padding=3)
multiplier += 1
ax.grid(axis='y'); ax.legend(ncols=3)
ax.set_ylim(0, 250)
# ax.set_xticks(x + width, species)
ax.set_xticks(x + ((width + spacing) * (multiplier - 1) / 2), species)
ax.set_ylabel('Length (mm)')
ax.set_title('Whitepaper plot')
plt.show()import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
species = ("Adelie", "Chinstrap", "Gentoo")
penguin_means = {
'Bill Depth': (18.35, 18.43, 14.98),
'Bill Length': (38.79, 48.83, 47.50),
'Flipper Length': (189.95, 195.82, 217.19),
}
x = np.arange(len(species)) # the label locations
width = 0.2 # the width of the bars
spacing = 0.0 # the space between bars within groups
multiplier = 0
with sns.color_palette('viridis', n_colors=3, as_cmap=False):
fig, ax = plt.subplots(layout='constrained', figsize=(6, 3.5))
for attribute, measurement in penguin_means.items():
offset = (width + spacing) * multiplier
rects = ax.barh(x + offset, measurement, height=width, alpha=.85,
label=attribute.lower().capitalize())
ax.bar_label(rects, padding=3)
multiplier += 1
ax.grid(axis='x')
ax.legend(ncols=3)
ax.set_xlim(0, 250)
ax.set_yticks(x + ((width + spacing) * (multiplier - 1) / 2))
ax.set_yticklabels(species)
ax.set_xlabel('Length (mm)')
ax.set_title('Transposed whitepaper plot')
plt.show()6 Grid
import matplotlib.pyplot as plt
import numpy as np
# At least one dimension must be > 1
N_ROWS = 2
N_COLS = 3
# Sample data for each subplot in groups of 2
x = np.linspace(0, 2 * np.pi, 100)
functions = []
titles = []
for i in range(N_ROWS*N_COLS * 2):
functions.append(lambda x: np.sin((i + 1) * x))
functions.append(lambda x: np.cos((i + 1) * x))
if (i % 2 == 0): titles.append(f'$a = {int(i/2 + 1)}$')
# Create a 2x2 subplots grid using a for loop
fig, axs = plt.subplots(N_ROWS, N_COLS, sharey=True)
# Flatten the axs array for easier iteration
axs = axs.flatten()
# Loop through subplots and plot data
for i, ax in enumerate(axs):
y1 = functions[i * 2](x)
y2 = functions[(i * 2) + 1](x)
ax.plot(x, y1)
ax.plot(x, y2)
# To add legend to each frame
# ax.legend(labels=[f'$sin({i + 1}x)$', f'$cos({i + 1}x)$'], loc=2)
# Set title of each frame and label only rows and columns
ax.set_title(titles[i])
if (i > (N_ROWS - 1) * N_COLS - 1): ax.set_xlabel('$x$')
if i % N_COLS == 0: ax.set_ylabel('$y$')
ax.grid()
# Add legend for groups
fig.legend(labels=['$sin(ax)$', '$cos(ax)$'], bbox_to_anchor=(1, .89), loc=2)
# Use tight layout (default) to prevent clipping of titles & center
fig.supylabel('$y$')
fig.supxlabel('$x$', x=.58)
plt.suptitle('Subplot grid', x=.58)
plt.show()7 Seaborn extensions for statistical plotting
import seaborn as sns
from matplotlib.ticker import StrMethodFormatter
data = sns.load_dataset("iris")
data_ = data.rename(columns=lambda name: name.replace('_', ' ').capitalize())
hist_kws = dict(edgecolor='black', linewidth=.5) # bins
kde_kws = dict(linewidth=.5)
scatter_kws = dict(alpha=.6, edgecolor='black', linewidth=.1) # s
line_kws = dict(linewidth=1)
reg_kws = dict(scatter_kws=scatter_kws, line_kws=line_kws)
with sns.axes_style('whitegrid'), sns.color_palette('viridis'):
# plt.figure(figsize=(6, 6))
ax = sns.pairplot(data_, vars=['Petal width', 'Petal length', 'Sepal length'],
hue='Species',
kind='reg', diag_kind='kde',
plot_kws=reg_kws, diag_kws=kde_kws,
)
plt.suptitle('Grouped pairplot')
plt.tight_layout()
plt.show()
# ax.axes.set_major_formatter(StrMethodFormatter(f'{{x:.2f}}'))
# sns.move_legend(ax, "upper left", bbox_to_anchor=(1, .75))# Grouped boxplots
# [TODO] add sigstars to significant within-group differences
tips = sns.load_dataset('tips')
# with sns.axes_style('whitegrid'), sns.color_palette('viridis', n_colors=2):
# with sns.color_palette('viridis', n_colors=2):
plt.figure()
ax = sns.boxplot(data=tips, x='day', y='total_bill', hue='sex',
# dodge=1,
gap=.2, width=.6,
saturation=.7,
fliersize=3.75,
# whis=.5,
# linecolor='black', linewidth=.5,
)
# plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
ax.grid(axis='y')
ax.legend(ncol=2, loc='best')
plt.xlabel('Category'); plt.ylabel('Value')
plt.title('Grouped boxplots')
plt.tight_layout()
plt.show()titanic = sns.load_dataset("titanic")
with sns.axes_style('whitegrid'):
plt.figure()
ax = sns.FacetGrid(titanic, col="survived", row="sex")
ax = ax.map(plt.hist, "age", alpha=.85, bins=10)
ax.set_xlabels('Age')
plt.suptitle('Bifaceted wildcard plot')
# plt.tight_layout()
plt.show()8 Additional seaborn plots
[TODO]
Missing 1. overlapping densities 2. overlapping scatter 3. jointplot 4. √ bars with error bar 5. timeseries w/ error bar
tips = sns.load_dataset('tips')
# hist_kws = dict(edgecolor='black', linewidth=.5) # bins
line_kws = dict(linewidth=1)
kde_kws = dict() # linewidth=.5
with sns.axes_style('whitegrid'):
plt.figure()
ax = sns.histplot(data=tips, x='total_bill', #hue='sex',
kde=True, element='bars', stat='count',
line_kws=line_kws, kde_kws=kde_kws,
)
plt.xlim(-10, 60)
plt.xlabel('Value')
plt.title('Histogram with KDE')
plt.tight_layout()
plt.show()# Correlation matrix and heatmap
# [TODO] Make these colours nicer
iris = sns.load_dataset('iris')
iris_ = iris.rename(columns=lambda name: name.replace('_', ' ').capitalize())
correlation_matrix = iris_.corr(numeric_only=True)
#with sns.plotting_context(font_scale=.1):
plt.figure()
ax = sns.heatmap(correlation_matrix,
annot=True, cbar=True, cmap=plt.cm.PiYG,
square=True,
linewidths=0,
#linecolor='black', edgecolor='black',
)
plt.title('Heatmap')
plt.show()9 Math
[TODO]
Missing 1. 3D scatter 2. 2D cartesian 3. 2surface 4. curve 5. 22D vector field 6. 2D contour plot
ML plots: 7. [TODO] 3D data + PCs -> transformed 2D 8. [TODO] clean up generative (HoML), cluster/DR comparison
Functionalize: 12. [TODO] functionalize ML plots (args: fit model; X/y train/test (test optional); DR/manifold method) 13. [TODO] functionalize ML comparisons (args: model builds, labs, dataset lists; DR/man meth; dataset kwargs)
[Multi] For class/clust functions: 14. [TODO] add support for multi-class via appropriate custom colour generator calls 15. [TODO] add support for multi-feature class/clust via appropriate DR/manifold method (class DR, clust man)
[Prep] For class/clust/manifold functions: 16. [TODO] include appropriate prep for each feature (num: scale, cat: enc, ts: smooth, word: embed, sent: tfidf)
[Datasets] For ML comparison * class/clust functions: 17. [TODO] include std set of datasets (blob/circ/lin) * std args (blob cov kw: sphere/elip/ndiag, deg over, rand)
Later, for model-specific validations: - fix standard dataset & DR/manifold method & prep
iris = sns.load_dataset('iris')
with sns.axes_style('whitegrid'):
plt.figure()
sns.kdeplot(data=iris, x='sepal_length', y='sepal_width',
cmap='Blues', fill=True, levels=5,
)
plt.title('Joint contour plot')
plt.xlabel('Feature 1'); plt.ylabel('Feature 2')
plt.tight_layout()
plt.show()10 Analysis
[TODO]
def math_plotter(
f: lambda {
function(x, y), curve(t), surface(u, v), field(x, y, z)},
type: string {
'2D', '3D', 'contour', 'curve', 'surface', 'field'},
coordinates: string = 'rect' {
'rect', 'radial', 'cylindrical', 'spherical'},
bounds: List(
{x, t, u}: List(lo: float, hi: float) = [-10., 10.],
{y, v}: List(lo: float, hi: float) = [-10., 10.],
{z}: List(lo: float, hi: float) = [-10., 10.])
) -> plot: mpl_object {
f_plot: mpl_subplot,
gradient_plot: mpl_subplot = None,
integral_{plot, text} (explicit 2D graph if '2D' type given and closed form exists; else numerical estimate wrt some specified bounds):
{mpl_subplot, string} = None}import numpy as np
import matplotlib.pyplot as plt
def f(x, y):
return np.sin(x) * np.cos(y)
# Create a grid of points & corresponding smaller grid for a neater quiver plot
n = 100
X, Y = np.meshgrid(np.linspace(-5, 5, n), np.linspace(-5, 5, n))
# X_quiv, Y_quiv = np.meshgrid(np.linspace(-5, 5, int(n/10)),
# np.linspace(-5, 5, int(n/10)))
# Compute the derivative of the surface
Z = f(X, Y)
# Z_quiv = f(X_quiv, Y_quiv)
dx, dy = np.gradient(Z)
# dx, dy = np.gradient(Z_quiv)
# Plot the surface and its derivative
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')
ax.quiver(X, Y, Z, dx, dy, np.zeros_like(dx),
arrow_length_ratio=.3, color='red')
# Set the axes labels
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
# Show the plot
plt.show()from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
import scipy.integrate as integrate
# Calculate \int^\infty_0 e^{-x} dx
# invexp = lambda x: np.exp(-x)
# integrate.quad(invexp, 0, np.inf)
# function = lambda x, y: x**2 + y**2
# integrate.quad(function, 0, np.inf)
def integral(x, y):
# return integrate.quad(lambda t: np.sqrt((x**2 + y**2 - 2*x*y*np.cos(np.pi*t*(np.sqrt(1/x**3) - np.sqrt(1/y**3))))/(x**3*y**3)), 0, np.sqrt(x**3*y**3))[0]
return integrate.quad(lambda t: t*x**2 + t*y**2, 0, x**2 + y**2)[0]
# X = np.arange(0.1, 5, 0.1)
# Y = np.arange(0.1, 5, 0.1)
X = np.arange(-10, 10, .1)
Y = np.arange(-10, 10, .1)
X, Y = np.meshgrid(X, Y)
Z = np.vectorize(integral)(X, Y)
fig = plt.figure()
ax = plt.axes(projection="3d")
ax.plot_wireframe(X, Y, Z, color='green')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1,
norm=plt.Normalize(np.nanmin(Z), np.nanmax(Z)),
cmap='winter', edgecolor='none')
# ax.set_xlim(-10, 10); ax.set_ylim(-10, 10); ax.set_zlim(-10, 10)
plt.show()11 Stats
[TODO] Plot common 2/3D dists alongside estimated: - mean/variance - probability wrt some specified bounds
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
random_seed=1000
# Distribution params (3 covariance options, shared mean)
cov_val = [-0.8, 0, 0.8]
mean = np.array([0,0])
# Container for density functions for further analysis
pdf_list = []
## Plot densities
ax = plt.figure(figsize=(8,6))
# iterate over different covariance values
for idx, val in enumerate(cov_val):
# Initialize the covariance matrix
cov = np.array([[1, val], [val, 1]])
# Generate Gaussian bivariate dist with given mean and covariance matrix
distr = multivariate_normal(cov = cov, mean = mean,
seed = random_seed)
# Generate a meshgrid complacent with the 3-sigma boundary
mean_1, mean_2 = mean[0], mean[1]
sigma_1, sigma_2 = cov[0,0], cov[1,1]
x = np.linspace(-3*sigma_1, 3*sigma_1, num=100)
y = np.linspace(-3*sigma_2, 3*sigma_2, num=100)
X, Y = np.meshgrid(x,y)
# Evaluate density for each point in the meshgrid
pdf = np.zeros(X.shape)
for i in range(X.shape[0]):
for j in range(X.shape[1]):
pdf[i,j] = distr.pdf([X[i,j], Y[i,j]])
pdf_list.append(pdf)
# Plot density function values
ax = plt.subplot(1, 3, idx + 1, projection = '3d')
ax.plot_surface(X, Y, pdf, cmap = 'viridis')
ax.axes.zaxis.set_ticks([])
# plt.xlabel("$x_1$")
# plt.ylabel("$x_2$")
#plt.title(f'Covariance between x1 and x2 = {val}')
plt.tight_layout()
plt.show()
## Plot contour maps
ax = plt.figure(figsize=(8,6))
for idx, val in enumerate(pdf_list):
plt.subplot(2, 3, idx + 1, aspect=1)
plt.contourf(X, Y, val, cmap='viridis')
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
#plt.title(f'Covariance between x1 and x2 = {cov_val[idx]}')
plt.tight_layout()
plt.show()12 Classifier deep-dive
### Groundwork (data, preprocess, decompose, model, and datashape inspection
import numpy as np
from timeit import default_timer as timer
from sklearn import datasets
from sklearn import linear_model, naive_bayes, svm, tree, ensemble
from sklearn.neural_network import MLPClassifier
from sklearn.decomposition import PCA, KernelPCA
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, accuracy_score
# Mutable parameters and obtain colourmap
n_features = 7
n_classes = 5
# higher resolutions reduce pixelation and thin out decision boundary (300)
resolution = 300
# higher values crowd plot (100)
n_samples=1000
cmap = cmr.get_sub_cmap('gnuplot2', .1, .8, N=n_classes)
color_list = [cmap(i)[:3] for i in range(cmap.N)]
# ListedColormap(color_list)
#
# (1) Make data
X, y = datasets.make_classification(
n_samples=n_samples, n_features=n_features,
n_informative=n_features, n_redundant=0,
n_clusters_per_class=1, n_classes=n_classes,
random_state=42,
)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.2,
random_state=42)
# (2) Preprocess, decompose and project feature space for later plotting
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X_train)
# dr_model = PCA(n_components=2)
dr_model = KernelPCA(n_components=2, fit_inverse_transform=True)
X2D = dr_model.fit_transform(scaler.fit_transform(X_train))
# (3) Build, fit
# model = linear_model.LogisticRegression()
model = naive_bayes.GaussianNB()
# model = svm.SVC(kernel='rbf', C=6, probability=True, random_state=42)
# model = tree.DecisionTreeClassifier(max_depth=100)
# model = ensemble.RandomForestClassifier(n_estimators=100, max_depth=100, criterion='gini')
# model = MLPClassifier(
# hidden_layer_sizes=np.size(X_train, 1) * 1,
# activation='relu', solver='adam',
# batch_size=round(.01 * len(X)),
# alpha=.001, momentum=.9
# )
t_start = timer()
model.fit(X_scaled, y_train)
t_end = timer()
t_elapsed = round(t_end - t_start, 4)
# Get projected scatter boundaries for plotting
x_min = X2D[:, 0].min() - 0.1 * (X2D[:, 0].max() - X2D[:, 0].min())
x_max = X2D[:, 0].max() + 0.1 * (X2D[:, 0].max() - X2D[:, 0].min())
y_min = X2D[:, 1].min() - 0.1 * (X2D[:, 1].max() - X2D[:, 1].min())
y_max = X2D[:, 1].max() + 0.1 * (X2D[:, 1].max() - X2D[:, 1].min())
xrg = [x_min, x_max]; yrg = [y_min, y_max]
axis = [x_min, x_max, y_min, y_max]
# (4a) Define projected inference grid wrt original feature space (inversion)
xx, yy = np.meshgrid(
np.arange(x_min, x_max, 1. * (x_max - x_min) / resolution),
np.arange(y_min, y_max, 1. * (y_max - y_min) / resolution)
)
X_grid = np.c_[xx.ravel(), yy.ravel()]
X_grid_inverse = scaler.inverse_transform(dr_model.inverse_transform(X_grid))
# assert np.all(list(zip(np.ravel(xx), np.ravel(yy))) == X_grid)
# (4b) Get probabilistic and deterministic predictions over inference grid
Zpp = model.predict_proba(X_grid_inverse)
Zp = model.predict(X_grid_inverse)
# Z = svm.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]
# (P1) Obtain decision boundary line within projected feature space
# as [...]
Zp_grid = Zp.reshape(xx.shape)
Zb = np.zeros(xx.shape)
Zb[:-1, :] = np.maximum((Zp_grid[:-1, :] != Zp_grid[1:, :]), Zb[:-1, :])
Zb[1:, :] = np.maximum((Zp_grid[:-1, :] != Zp_grid[1:, :]), Zb[1:, :])
Zb[:, :-1] = np.maximum((Zp_grid[:, :-1] != Zp_grid[:, 1:]), Zb[:, :-1])
Zb[:, 1:] = np.maximum((Zp_grid[:, :-1] != Zp_grid[:, 1:]), Zb[:, 1:])
# (P2) Obtain graded probability surface within projected feature space
# as [(n_samples, n_classes) probability surface] * [(n_classes, 3) color vec]
# yielding (Zp_grid size) grid with RGB color vector values
colors = np.array(color_list[0:n_classes])
zz = np.dot(Zpp, colors)
zz_r = zz.reshape(xx.shape[0], xx.shape[1], colors.shape[1])
#
# (1-2) Attributes, Targets > Features > Decomposed features >
# (4a) Inference grid, Ravelled into features, Inverted to og feature space >
# (4b) Probabilistic + Deterministic predictions,
# (P1) Unravelled into grid for plotting > Decision boundary line >
# (P2) Colour-graded probability surface
display('X', 'y', 'X_scaled', 'X2D',
'xx', 'yy', 'X_grid', 'X_grid_inverse',
'Zpp', 'Zp',
'Zp_grid', '(Zp_grid[:-1, :])', '(Zp_grid[1:, :])', '(Zb[:-1, :])', 'Zb',
'colors', 'zz', 'zz_r',
)### Plotting: illustrative plot of probability surface
# [TODO] implement cross-validation here instead of a single train/test split
# [TODO] define search grids for each model and complexity knobs for val
# [TODO] pipe prep & model & plot grid/rand search results below as heat or lol
# [TODO] plot training/validation curve & learning curve below on 1 line
# [TODO] incorporate all models from sklearn classifier comparison plot
# [TODO] repeat for clustering, manifold
import matplotlib.patches as mpatches
axis_lim = [min(xrg[0], yrg[0]), max(xrg[1], yrg[1])]
axis_equal = axis_lim + axis_lim
# Prep test data identically to training data, evaluate
X_scaled_test = scaler.fit_transform(X_test)
y_pred = model.predict(X_scaled_test)
accuracy_val = accuracy_score(y_pred=y_pred, y_true=y_test)
y_pred_train = model.predict(X_scaled)
accuracy_train = accuracy_score(y_pred=y_pred_train, y_true=y_train)
X2D_test = dr_model.fit_transform(X_scaled_test)
#
fig, ax = plt.subplots(1, 1, figsize=(6,6))
# Boundary line
ax.imshow(Zb, origin='lower', interpolation=None, cmap='Greys',
alpha=1.0, extent=axis_equal)
# Probability surface
ax.imshow(zz_r, origin='lower', interpolation=None,
alpha=.7, extent=axis_equal)
# Scatter
ax.scatter(X2D[:, 0], X2D[:, 1], c=[colors[i, :] for i in y_train],
# linewidths=.5, edgecolors='k',
)
#
# Add legend
colors_bar = []
for v1 in colors[:n_classes, :]:
v1 = list(v1)
v1.append(.7)
colors_bar.append(v1)
# create a patch (proxy artist) for every color
patches = [mpatches.Patch(color=colors_bar[i],
label="Class {k}".format(k=i))
for i in range(n_classes)]
# put those patched as legend-handles into the legend
plt.legend(handles=patches, bbox_to_anchor=(1.05, 1),
loc=2, borderaxespad=0., framealpha=0.5)
plt.grid()
# ax.set_aspect('equal', adjustable='box')
ax.set_xlim(axis_lim)
ax.set_ylim(axis_lim)
if dr_model is None:
plt.xlabel('Raw axis $x_1$')
plt.ylabel('Raw axis $x_2$')
else:
plt.xlabel('Dimension reduced axis 1')
plt.ylabel('Dimension reduced axis 2')
ax.set_title(f"{str(model)[:]}\ndecision surface", size=10)
ax.text(
axis_lim[1] - 0.3, axis_lim[0] + 0.3,
f"Training accuracy: {accuracy_train}, Validation accuracy: {accuracy_val}\n\
Training time: {t_elapsed}s",
size=9,
horizontalalignment="right",
bbox=dict(boxstyle="round", alpha=0.8, facecolor="white"),
# transform=ax.transAxes,
)
plt.suptitle(
f"{n_classes} classes by {n_features} features\n\
{len(X_train)} training samples, {len(X_test)} testing samples",
x=1 - .4, y=0 + .025,
# ha='center', va='bottom',
)
# Training accuracy: {accuracy_train}, Validation accuracy: {accuracy_val}\n\
# Training time: {t_elapsed} s",
plt.show()
# confusion_matrix(y_pred=y_pred, y_true=y_test)
confusion_matrix(y_pred=y_pred_train, y_true=y_train)13 ML
# 2-class classifier plot with decision boundary
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
import seaborn as sns
from sklearn.datasets import make_classification
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
# Make data and preprocess
n_classes = 2
X, y = make_classification(n_samples=500, n_features=2,
n_informative=2, n_redundant=0,
n_clusters_per_class=1, n_classes=n_classes,
)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# Build classifier, fit, and predict
svm = SVC(kernel='rbf', random_state=42, probability=True)
svm.fit(X_scaled, y)
xx, yy = np.meshgrid(np.linspace(-3, 3, 100), np.linspace(-3, 3, 100))
Z = svm.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]
Z = Z.reshape(xx.shape)
# Plot scatter with decision surface
with sns.axes_style('whitegrid'):
plt.figure()
plt.contourf(xx, yy, Z, cmap='PiYG', alpha=0.8) # cmap='coolwarm'
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=y,
cmap=ListedColormap(["#b30065", "#178000"]),
# cmap=cmr.get_sub_cmap('PiYG', .1, .9, N=n_classes),
# cmap='viridis',
)
plt.grid()
plt.xlim(-3, 3); plt.ylim(-3, 3)
plt.xlabel('Feature 1'); plt.ylabel('Feature 2')
plt.title('2-class classifier with scatter and decision surface')
plt.show()import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, svm
from sklearn.inspection import DecisionBoundaryDisplay
# Data
iris = datasets.load_iris()
X = iris.data[:, :2] # only take first two features
Y = iris.target # 3 classes
# Build classifier & fit
clf = svm.SVC(kernel='rbf')
clf.fit(X, Y)
# Plot model
# h = 0.02 # step size in the mesh
with sns.axes_style('whitegrid'):
plt.figure()
ax = plt.gca()
DecisionBoundaryDisplay.from_estimator(
clf, X, ax=ax,
cmap=plt.cm.viridis_r, grid_resolution=100,
response_method="predict", plot_method="pcolormesh", shading="auto",
alpha=.85
)
# Plot scatter
plt.scatter(X[:, 0], X[:, 1], c=Y, s=20,
cmap=plt.cm.viridis_r, edgecolors="k", linewidths=1, alpha=.85,
)
plt.xlabel('Feature 1'); plt.ylabel('Feature 2')
plt.title("3-class classifier with scatter and decision boundary")
plt.axis("tight")
plt.show()# Generative kernels and graded densities
from sklearn.datasets import make_blobs
from sklearn.mixture import GaussianMixture
from sklearn.preprocessing import StandardScaler
# Get data & preprocess
X, y = make_blobs(n_samples=500, centers=3, random_state=42, cluster_std=3.0)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# Model & fit
gmm = GaussianMixture(n_components=3, random_state=42)
gmm.fit(X_scaled)
# Build grid & predict
h = 0.02
x_min, x_max = X_scaled[:, 0].min() - 1, X_scaled[:, 0].max() + 1
y_min, y_max = X_scaled[:, 1].min() - 1, X_scaled[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = -gmm.score_samples(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot model & scatter
with sns.axes_style('whitegrid'):
plt.figure()
plt.contourf(xx, yy, Z, levels=20, alpha=0.8, cmap='viridis')
scatter = sns.scatterplot(
x=X_scaled[:, 0], y=X_scaled[:, 1], hue=y, s=20,
palette='pastel', edgecolor='black', alpha=.9,
)
# Plot centers
plt.scatter(
gmm.means_[:, 0], gmm.means_[:, 1],
# color='red', marker='o', s=30, alpha=.85,
color='white', marker='o', s=75,
edgecolor='black', linewidths=.5,
)
plt.xlabel('Feature 1'); plt.ylabel('Feature 2')
plt.xlim(x_min, x_max); plt.ylim(y_min, y_max)
plt.title('3-class clustering with scatter and densities')
handles, labels = scatter.get_legend_handles_labels()
plt.legend(handles, ['Cluster ' + item for item in labels],
loc='best', #bbox_to_anchor=(1, 0.5),
frameon=1,
)
plt.show()14 Model comparison routines (dataset x model/hyperparameter)
# Code source: Gaël Varoquaux
# Andreas Müller
# Modified for documentation by Jaques Grobler
# License: BSD 3 clause
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import ListedColormap
from sklearn.datasets import make_circles, make_classification, make_moons
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
from sklearn.ensemble import AdaBoostClassifier, RandomForestClassifier
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF
from sklearn.inspection import DecisionBoundaryDisplay
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.neighbors import KNeighborsClassifier
from sklearn.neural_network import MLPClassifier
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
## Make models
names = [
# "Nearest Neighbors",
# "Linear SVM",
"RBF SVM",
# "Gaussian Process",
"Decision Tree",
"Random Forest",
"Neural Net",
# "AdaBoost",
"Naive Bayes",
# "QDA",
]
classifiers = [
# KNeighborsClassifier(3),
# SVC(kernel="linear", C=0.025, random_state=42),
SVC(gamma=2, C=1, random_state=42),
# GaussianProcessClassifier(1.0 * RBF(1.0), random_state=42),
DecisionTreeClassifier(max_depth=5, random_state=42),
RandomForestClassifier(
max_depth=5, n_estimators=10, max_features=1, random_state=42
),
MLPClassifier(alpha=1, max_iter=1000, random_state=42),
# AdaBoostClassifier(algorithm="SAMME", random_state=42),
GaussianNB(),
# QuadraticDiscriminantAnalysis(),
]
## Make datasets
X, y = make_classification(
n_features=2, n_redundant=0, n_informative=2, random_state=1, n_clusters_per_class=1
)
rng = np.random.RandomState(2)
X += 2 * rng.uniform(size=X.shape)
linearly_separable = (X, y)
datasets = [
make_moons(noise=0.3, random_state=0),
make_circles(noise=0.2, factor=0.5, random_state=1),
linearly_separable,
]
## Plot
figure = plt.figure(figsize=(8, 6)) # figure = plt.figure(figsize=(27, 9))
# iterate over datasets
i = 1
for ds_cnt, ds in enumerate(datasets):
## Split into training and test part
X, y = ds
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.4, random_state=42
)
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
## Plot the dataset
cm = plt.cm.PiYG # cm = plt.cm.RdBu
cm_bright = ListedColormap(["#b30065", "#178000"]) # cm_bright = ListedColormap(["#FF0000", "#0000FF"])
ax = plt.subplot(len(datasets), len(classifiers) + 1, i)
if ds_cnt == 0:
ax.set_title("Input data")
# Plot the training points & testing points (latter slightly faded)
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train,
cmap=cm_bright, edgecolors="k",
)
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test,
cmap=cm_bright, edgecolors="k", alpha=0.6,
)
# Plotting adjustments
ax.set_xlim(x_min, x_max)
ax.set_ylim(y_min, y_max)
ax.set_xticks(())
ax.set_yticks(())
i += 1
# iterate over classifiers
for name, clf in zip(names, classifiers):
ax = plt.subplot(len(datasets), len(classifiers) + 1, i)
## Preprocess, fit, and plot fit
clf = make_pipeline(StandardScaler(), clf)
clf.fit(X_train, y_train)
score = clf.score(X_test, y_test)
DecisionBoundaryDisplay.from_estimator(
clf, X, cmap=cm, alpha=0.8, ax=ax, eps=0.5
)
# Plot the training points & testing points (latter slightly faded)
ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train,
cmap=cm_bright, edgecolors="k",
)
ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test,
cmap=cm_bright, edgecolors="k", alpha=0.6,
)
# Plotting adjustments & annotation
ax.set_xlim(x_min, x_max)
ax.set_ylim(y_min, y_max)
ax.set_xticks(())
ax.set_yticks(())
if ds_cnt == 0:
ax.set_title(name)
ax.text(
x_max - 0.3,
y_min + 0.3,
("%.2f" % score).lstrip("0"),
size=12,
horizontalalignment="right",
bbox=dict(boxstyle="round", alpha=0.8, facecolor="white"),
# transform=ax.transAxes,
)
i += 1
figure.suptitle('Classifier comparison')
# figure.supxlabel('x')
# figure.supylabel('y')
plt.tight_layout()
plt.show()# [TODO] polish this
import time
import warnings
from itertools import cycle, islice
import matplotlib.pyplot as plt
import numpy as np
from sklearn import cluster, datasets, mixture
from sklearn.neighbors import kneighbors_graph
from sklearn.preprocessing import StandardScaler
# ============
# Generate datasets. We choose the size big enough to see the scalability
# of the algorithms, but not too big to avoid too long running times
# ============
n_samples = 500
seed = 30
noisy_circles = datasets.make_circles(
n_samples=n_samples, factor=0.5, noise=0.05, random_state=seed
)
noisy_moons = datasets.make_moons(n_samples=n_samples, noise=0.05, random_state=seed)
blobs = datasets.make_blobs(n_samples=n_samples, random_state=seed)
rng = np.random.RandomState(seed)
no_structure = rng.rand(n_samples, 2), None
# Anisotropicly distributed data
random_state = 170
X, y = datasets.make_blobs(n_samples=n_samples, random_state=random_state)
transformation = [[0.6, -0.6], [-0.4, 0.8]]
X_aniso = np.dot(X, transformation)
aniso = (X_aniso, y)
# blobs with varied variances
varied = datasets.make_blobs(
n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5], random_state=random_state
)
# ============
# Set up cluster parameters
# ============
plt.figure(figsize=(12, 8)) # (9 * 2 + 3, 13)
plt.subplots_adjust(
left=0.02, right=0.98, bottom=0.001, top=0.95, wspace=0.05, hspace=0.01
)
plot_num = 1
default_base = {
"quantile": 0.3,
"eps": 0.3,
"damping": 0.9,
"preference": -200,
"n_neighbors": 3,
"n_clusters": 3,
"min_samples": 7,
"xi": 0.05,
"min_cluster_size": 0.1,
"allow_single_cluster": True,
"hdbscan_min_cluster_size": 15,
"hdbscan_min_samples": 3,
"random_state": 42,
}
datasets = [
(
noisy_circles,
{
"damping": 0.77,
"preference": -240,
"quantile": 0.2,
"n_clusters": 2,
"min_samples": 7,
"xi": 0.08,
},
),
(
noisy_moons,
{
"damping": 0.75,
"preference": -220,
"n_clusters": 2,
"min_samples": 7,
"xi": 0.1,
},
),
(
varied,
{
"eps": 0.18,
"n_neighbors": 2,
"min_samples": 7,
"xi": 0.01,
"min_cluster_size": 0.2,
},
),
(
aniso,
{
"eps": 0.15,
"n_neighbors": 2,
"min_samples": 7,
"xi": 0.1,
"min_cluster_size": 0.2,
},
),
(blobs, {"min_samples": 7, "xi": 0.1, "min_cluster_size": 0.2}),
(no_structure, {}),
]
for i_dataset, (dataset, algo_params) in enumerate(datasets):
# update parameters with dataset-specific values
params = default_base.copy()
params.update(algo_params)
X, y = dataset
# normalize dataset for easier parameter selection
X = StandardScaler().fit_transform(X)
# estimate bandwidth for mean shift
bandwidth = cluster.estimate_bandwidth(X, quantile=params["quantile"])
# connectivity matrix for structured Ward
connectivity = kneighbors_graph(
X, n_neighbors=params["n_neighbors"], include_self=False
)
# make connectivity symmetric
connectivity = 0.5 * (connectivity + connectivity.T)
# ============
# Create cluster objects
# ============
ms = cluster.MeanShift(bandwidth=bandwidth, bin_seeding=True)
two_means = cluster.MiniBatchKMeans(
n_clusters=params["n_clusters"],
random_state=params["random_state"],
)
ward = cluster.AgglomerativeClustering(
n_clusters=params["n_clusters"], linkage="ward", connectivity=connectivity
)
spectral = cluster.SpectralClustering(
n_clusters=params["n_clusters"],
eigen_solver="arpack",
affinity="nearest_neighbors",
random_state=params["random_state"],
)
dbscan = cluster.DBSCAN(eps=params["eps"])
# hdbscan = cluster.HDBSCAN(
# min_samples=params["hdbscan_min_samples"],
# min_cluster_size=params["hdbscan_min_cluster_size"],
# allow_single_cluster=params["allow_single_cluster"],
# )
optics = cluster.OPTICS(
min_samples=params["min_samples"],
xi=params["xi"],
min_cluster_size=params["min_cluster_size"],
)
affinity_propagation = cluster.AffinityPropagation(
damping=params["damping"],
preference=params["preference"],
random_state=params["random_state"],
)
average_linkage = cluster.AgglomerativeClustering(
linkage="average",
metric="cityblock",
n_clusters=params["n_clusters"],
connectivity=connectivity,
)
birch = cluster.Birch(n_clusters=params["n_clusters"])
gmm = mixture.GaussianMixture(
n_components=params["n_clusters"],
covariance_type="full",
random_state=params["random_state"],
)
clustering_algorithms = (
("MiniBatch\nKMeans", two_means),
("Affinity\nPropagation", affinity_propagation),
("MeanShift", ms),
("Spectral\nClustering", spectral),
("Ward", ward),
("Agglomerative\nClustering", average_linkage),
("DBSCAN", dbscan),
# ("HDBSCAN", hdbscan),
("OPTICS", optics),
("BIRCH", birch),
("Gaussian\nMixture", gmm),
)
for name, algorithm in clustering_algorithms:
t0 = time.time()
# catch warnings related to kneighbors_graph
with warnings.catch_warnings():
warnings.filterwarnings(
"ignore",
message="the number of connected components of the "
+ "connectivity matrix is [0-9]{1,2}"
+ " > 1. Completing it to avoid stopping the tree early.",
category=UserWarning,
)
warnings.filterwarnings(
"ignore",
message="Graph is not fully connected, spectral embedding"
+ " may not work as expected.",
category=UserWarning,
)
algorithm.fit(X)
t1 = time.time()
if hasattr(algorithm, "labels_"):
y_pred = algorithm.labels_.astype(int)
else:
y_pred = algorithm.predict(X)
plt.subplot(len(datasets), len(clustering_algorithms), plot_num)
if i_dataset == 0:
plt.title(name) # size=18
colors = np.array(
list(
islice(
cycle(
[
"#377eb8",
"#ff7f00",
"#4daf4a",
"#f781bf",
"#a65628",
"#984ea3",
"#999999",
"#e41a1c",
"#dede00",
]
),
int(max(y_pred) + 1),
)
)
)
# add black color for outliers (if any)
colors = np.append(colors, ["#000000"])
plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[y_pred])
plt.xlim(-2.5, 2.5)
plt.ylim(-2.5, 2.5)
plt.xticks(())
plt.yticks(())
plt.text(
0.99,
0.01,
("%.2fs" % (t1 - t0)).lstrip("0"),
transform=plt.gca().transAxes,
# size=15,
horizontalalignment="right",
)
plot_num += 1
plt.show()# [TODO] polish this
# Author: Jaques Grobler <jaques.grobler@inria.fr>
# License: BSD 3 clause
from time import time
import matplotlib.pyplot as plt
# Unused but required import for doing 3d projections with matplotlib < 3.2
import mpl_toolkits.mplot3d # noqa: F401
import numpy as np
from matplotlib.ticker import NullFormatter
from sklearn import manifold
from sklearn.utils import check_random_state
# Variables for manifold learning.
n_neighbors = 10
n_samples = 1000
# Create our sphere.
random_state = check_random_state(0)
p = random_state.rand(n_samples) * (2 * np.pi - 0.55)
t = random_state.rand(n_samples) * np.pi
# Sever the poles from the sphere.
indices = (t < (np.pi - (np.pi / 8))) & (t > ((np.pi / 8)))
colors = p[indices]
x, y, z = (
np.sin(t[indices]) * np.cos(p[indices]),
np.sin(t[indices]) * np.sin(p[indices]),
np.cos(t[indices]),
)
# Plot our dataset.
fig = plt.figure(figsize=(10, 6)) # (15, 8)
plt.suptitle(
"Manifold Learning with %i points, %i neighbors" % (1000, n_neighbors),
) # fontsize=14
ax = fig.add_subplot(251, projection="3d")
ax.scatter(x, y, z, c=p[indices], cmap=plt.cm.rainbow)
ax.view_init(40, -10)
sphere_data = np.array([x, y, z]).T
# Perform Locally Linear Embedding Manifold learning
methods = ["standard", "ltsa", "hessian", "modified"]
labels = ["LLE", "LTSA", "Hessian LLE", "Modified LLE"]
for i, method in enumerate(methods):
t0 = time()
trans_data = (
manifold.LocallyLinearEmbedding(
n_neighbors=n_neighbors, n_components=2, method=method, random_state=42
)
.fit_transform(sphere_data)
.T
)
t1 = time()
print("%s: %.2g sec" % (methods[i], t1 - t0))
ax = fig.add_subplot(252 + i)
plt.scatter(trans_data[0], trans_data[1], c=colors, cmap=plt.cm.rainbow)
plt.title("%s (%.2g sec)" % (labels[i], t1 - t0))
ax.xaxis.set_major_formatter(NullFormatter())
ax.yaxis.set_major_formatter(NullFormatter())
plt.axis("tight")
# Perform Isomap Manifold learning.
t0 = time()
trans_data = (
manifold.Isomap(n_neighbors=n_neighbors, n_components=2)
.fit_transform(sphere_data)
.T
)
t1 = time()
print("%s: %.2g sec" % ("ISO", t1 - t0))
ax = fig.add_subplot(257)
plt.scatter(trans_data[0], trans_data[1], c=colors, cmap=plt.cm.rainbow)
plt.title("%s (%.2g sec)" % ("Isomap", t1 - t0))
ax.xaxis.set_major_formatter(NullFormatter())
ax.yaxis.set_major_formatter(NullFormatter())
plt.axis("tight")
# Perform Multi-dimensional scaling.
t0 = time()
mds = manifold.MDS(2, max_iter=100, n_init=1, random_state=42)
trans_data = mds.fit_transform(sphere_data).T
t1 = time()
print("MDS: %.2g sec" % (t1 - t0))
ax = fig.add_subplot(258)
plt.scatter(trans_data[0], trans_data[1], c=colors, cmap=plt.cm.rainbow)
plt.title("MDS (%.2g sec)" % (t1 - t0))
ax.xaxis.set_major_formatter(NullFormatter())
ax.yaxis.set_major_formatter(NullFormatter())
plt.axis("tight")
# Perform Spectral Embedding.
t0 = time()
se = manifold.SpectralEmbedding(
n_components=2, n_neighbors=n_neighbors, random_state=42
)
trans_data = se.fit_transform(sphere_data).T
t1 = time()
print("Spectral Embedding: %.2g sec" % (t1 - t0))
ax = fig.add_subplot(259)
plt.scatter(trans_data[0], trans_data[1], c=colors, cmap=plt.cm.rainbow)
plt.title("Spectral Embedding (%.2g sec)" % (t1 - t0))
ax.xaxis.set_major_formatter(NullFormatter())
ax.yaxis.set_major_formatter(NullFormatter())
plt.axis("tight")
# Perform t-distributed stochastic neighbor embedding.
t0 = time()
tsne = manifold.TSNE(n_components=2, random_state=0)
trans_data = tsne.fit_transform(sphere_data).T
t1 = time()
print("t-SNE: %.2g sec" % (t1 - t0))
ax = fig.add_subplot(2, 5, 10)
plt.scatter(trans_data[0], trans_data[1], c=colors, cmap=plt.cm.rainbow)
plt.title("t-SNE (%.2g sec)" % (t1 - t0))
ax.xaxis.set_major_formatter(NullFormatter())
ax.yaxis.set_major_formatter(NullFormatter())
plt.axis("tight")
plt.show()